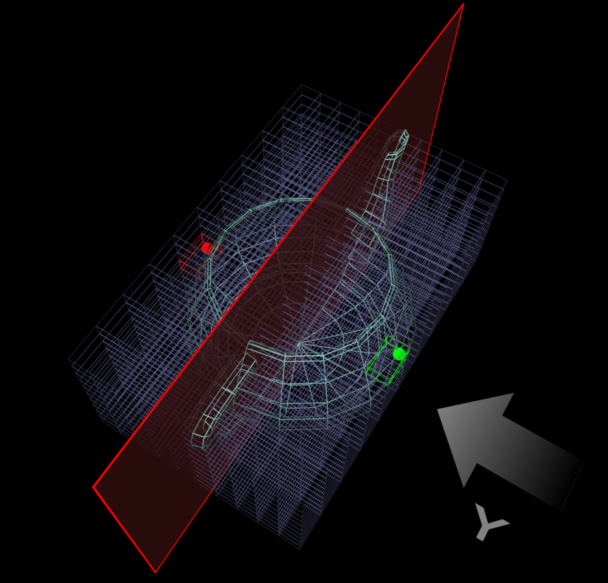
 |
-
The green point to
the right is the original selected vertex to be mirror-selected along the
Y axis.
-
The red pointis
the symmetrical vertex to be selected.
-
The red plane
shows the local XZ plane used as a plane of symmetry.
-
Symmetry divides the object space into Voxels
(Spatial SubDivisions). On the image, there are 10x10x10 Voxels, 1000 altogether.
Each vertex of the teapot is inside of exactly one Voxel, so are the green
and red vertices.
-
Symmetry writes down the indices of all vertices
found in each Voxel. This is the process called "Database Rebuilding".
This way by looking at only 1/1000 of the volume it can quickly find the
desired vertex without accessing all vertices in the mesh.
-
Symmetry finds the Voxel the green vertex
resides in (Voxel is shown in green, too).
-
Then it searches for the Voxel with spatial
coordinates that are symmetrical to the green Voxel - this Voxel (shown
in red) has the exactly same X and Z coordinates, but the Y
is mirrored relatively to the plane of symmetry.
-
Now that it knows which Voxel to check, it
can look at the Database and compare the positions of the few vertices
found in the current Voxel to the expected position of the symmetrical
vertex. If there is a vertex inside the threshold, it gets selected.
-
Face and Edge selections are handled at vertex
level. For each Edge, two vertex queries have to be performed. For a Quad,
there are four checks. If all of them return valid symmetry results, the
Edge/Face containing these symmetry vertices gets selected.
|



